25春-计算机图形学作业(留档)
一、判断题
光栅扫描显示器属于面线的设备。( √ )
Bresenham 直线光栅化算法比 DDA 算法的效率高。( √ )
走样现象被消除。( × )
解析:
走样(aliasing)只能通过抗锯齿技术减轻,但无法完全消除。
屏幕上最小的显示单元叫做像素。( √ )
种子填充算法中,四联通填充算法即可填充四联通区域,同时也可填充把联通区域。( × )
解析:
四联通只能填充 4-连通区域,无法填充存在仅 8-连通的区域。
多边形裁剪与直线裁剪没有本质的区别。( √ )
多边形的扫描线填充算法中,当扫描线与多边形某条边的交点坐标为整数时则直线将该交点的像素点点亮,无需取整运算。( × )
解析:
即便交点坐标为整数,也需考虑端点规则与偶奇性,仍要做判断和处理。
多边形的扫描线填充算法中,活动边表中结点个数表示当前扫描线与多边形相交的交点个数,算法进行过程中的任何时刻,该交点个数一定是偶数。()
Sutherland-Hudgman 多边形裁剪算法适用于裁剪多边形。( √ )
在进行多边形裁剪时,可以直接利用二进制裁剪算法或者参数化算法,对多边形的每条边裁剪即可。( × )
解析:
多边形裁剪要处理各顶点的插入与删除,不能简单地“逐边裁剪”而不作顶点连接处理。
二、单选题
Cohen-Sutherland 二进制编码裁剪算法,首先将平面分为( B )个区域进行编码,以方便对直线分情况处理。 A. 4 B. 9 C. 12 D. 27
解析:
窗口外部按上下左右及四个角共 8 个区域,加上窗口内部,共 9 个编码区。
假设直线段的两端点编码分别为 code1 和 code2,已知 code1、code2 不全为0000,且 code1 按位与 code2 不等于 0,则该直线属于( B )情况。 A. 取之 B. 弃之 C. 裁之 D. 无法判断
解析:
位与非零表示两端都在同一窗口外侧区域,可直接舍弃。
实现种子填充算法时,需要满足一定的前提条件,下面那个条件不是种子填充算法实现时必须的前提条件。( C ) A. 区域以边界表示法表示 B. 区域以内点表示法表示 C. 区城以顶点表示法表示 D. 区域边界颜色与内点颜色不同
解析:
只需有边界(或内点)和不同色,顶点表示法并非必需。
多边形的扫描线填充算法中,采用射线法判断扫描线与多边形交点的个数。当扫描线与多边形的顶点相交时,交点个数需特殊处理。下列说法错误的( C )。 A. 共享顶点的两条边分别位于扫描线的两侧,交点算一个 B. 共享顶点的两条边分别位于扫描线的下侧,交点算零个 C. 共享顶点的两条边分别位于扫描线的上侧,交点算两个 D. 共享顶点的两条边分别位于扫描线的两制,交点算两个
解析:
两条边都在上侧应算 0 个,不是 2 个。
平面中有一条直线段,起点P1(0.0)、终点P2(5,2),利用 DDA 算法扫描转换该直线,如果当前点亮的像素点(2,1),则下一次点亮的素点是( C )。
A. (2,1) B. (2,2) C. (3.1) D. (3,2)
解析:
斜率≈0.4,x 增 1,y 增≈0.4,1+0.4=1.4→舍入 1,故 (3,1)。
利用终点 Bresenham 算法对 4a 区间的直线进行扫描转换时,设当前点亮的像素点坐标为(x,y),当前判别式d > 0,则下一次将被带入判别式方程的中点 M 坐 标为( B )。 A. (x+1, y-0.5) B. (x+1, y+0.5) C. (x+2. y-15) D.(x+2, y+1.5)
解析:
d>0 时选择东北像素,对应下次判别点为 (x+1, y+0.5)。
在直线的光栅化算法中,最大位移方向指的是( C )。
A. x 方向
B. 当斜率大于 1 时,最大位移方向为 x 方向
C. x 方向和 y 方向中增量较大的方向
D. y 方向
解析:
选择 Δx、Δy 较大的一方向为主步进方向。
在直线的光栅化算法中,如果不考虑最大位移方向,则可能得到( C )的直线。 A. 斜率为 1 的 B. 总是垂直的 C. 离散的点,无法构成直线 D. 总是水平的
解析:
随机步进导致点分散,不成连续线段。
在直线的改进的 Bresenham 算法中,每当误差项 k 大于 0.5 以后必须让 k 减去 1,否期此后的直线将变成( C )。 A. 垂直的 B.不确定 C. 斜事绝对值为 1 的 D. 水平的
解析:
误差积累过大,y 每步都增 1,变成 45° 直线。
下列有关 Liang-Barsky 算法的叙述中,正确的论述是( C )。 A. Liang-Barsky 算法的思想是把被裁剪的线段看成是有向线段 B. 窗口入边的两个交点和被裁减直线的终点为一组,窗口出边的两个交点和被裁剪直线的起始点为一组 C. Liang-Barsky 算法的基本出发点是直线的点斜式方程 D. Liang-Barsky算法主要是针对凸多边形的裁剪算法
解析:
它直接利用参数方程 t 对 x,y 进行裁剪,故 C 正确。
三、多选题
下列论述( CD )是正确的 A. 矢量图与位图相比更容易模仿真实感图形效果 B. 位图文件存储空间比矢量文件小 C. 在图形缩放时,矢量图不失真 D. 互联网上常见的图形格式如 JPEG,属于位图格式
下列有关Liang-Barsky 算法的叙述中,错误的论述是( BC )
A. Liang-Barsky 算法的思想是把被裁剪的线段看成是有向线段
B. 在 Liang-Barsky 算法中,裁剪结果的线段起点是入边的两个交点和被裁线段始端点三个点里面,对应参数最小的一个点
C. Liang-Barsky 算法主要是针对凸多边形的裁剪算法
D. Liang-Barsky 算法的基本出发点是直线的参数式方程
在区域分割(Warnack)消隐算法中,窗口与多边形的关系包括( ABCD )
A. 包围 B.内含 C.分离 D.相交
下列有关走样、反走样的论述( BD )是正确的
A. 走样现象是可以完全消除的
B. 反走样技术主要由提高分辨率、非加权区域采样、加权区域采样等
C. 非加权区域采样技术一般优于加权区域采样技术
D. 走样现象不可能完全消除
下面关于深度缓存消隐算法(Z-Buffer)的论述,( CD )是正确的
A. Z-Buffer 算法是在像素级上的消隐算法,因此效率高
B. Z-Buffer 算法占用空间小
C. Z-Buffer 算法需要开辟一个与图像大小相等的深度缓存数组
D. Z-Buffer 算法没有利用图形的相关性与连续性
四、简答题
请陈述计算机图形学的应用并分析在未来的发展
解:
主要应用领域
虚拟现实与增强现实:在游戏、仿真训练(飞行、医疗)中生成沉浸式图像;
影视与动画:电影特效、三维动画制作依赖高级渲染和物理仿真;
CAD/CAM:工程制图、逆向建模、数控加工路径规划;
医疗成像:三维重建、手术导航、MRI/CT 可视化;
地理信息系统(GIS):地形建模、地图渲染、空间分析可视化。
未来发展趋势
实时光线追踪普及:GPU 硬件和 API(如 DirectX Raytracing、OptiX)加速,将实现实时光线追踪渲染;
基于物理的渲染(PBR):更真实的材料和光照模型,加上机器学习降噪技术,逼真度大幅提升;
AI 与图形融合:神经渲染、图像生成网络(如 NeRF)、AI 辅助建模与贴图;
大规模点云与体数据可视化:自动驾驶、智慧城市背景下,海量三维数据的交互渲染;
跨平台轻量化渲染引擎:移动端、WebGL/WebGPU 的高性能三维显示。
五、计算题
请用中点画线算法绘制直线y=2x+1,其中x的范围是[0,10]
解:
该直线斜率正好为 2,函数值在整数点上恰好也是整数,故中点算法每步都选上方像素。输出的离散点为:
x y = 2x+1 像素点 (x, y) 0 1 (0, 1) 1 3 (1, 3) 2 5 (2, 5) 3 7 (3, 7) 4 9 (4, 9) 5 11 (5, 11) 6 13 (6, 13) 7 15 (7, 15) 8 17 (8, 17) 9 19 (9, 19) 10 21 (10, 21) 注: 因为 yyy 在每个整数 xxx 上都为整数,算法直接选择该像素,无需在两像素间取舍。
请用 DDA 扫描转换连接两点 P_0(0,0) 和 P_1(5,3) 的直线段
解:
Δx=5, Δy=3, steps=max(5,3)=5
x_{inc} = 5/5 =1,y_{inc}=3/5=0.6
起点 (x,y)=(0,0),每步累加并四舍五入:
步骤 k 理想坐标 (x_k,y_k) 像素点(round(x_k),round(y_k)) 0 (0.0, 0.0) (0, 0) 1 (1.0, 0.6) (1, 1) 2 (2.0, 1.2) (2, 1) 3 (3.0, 1.8) (3, 2) 4 (4.0, 2.4) (4, 2) 5 (5.0, 3.0) (5, 3) 这样就完成了 DDA 扫描转换。
随堂卷Ⅱ
一、单选题
在下列叙述语句中,错误的论述为( C ) A. 在图形文件系统中,点、线、圆等图形元素通常都用其几何特征参数来描述 B. 在图形系统中,图形处理运算的精度不取决于显示器的分辨率 C. 在光栅扫描图形显示器中所有图形都按矢量直接描绘显示,不存在任何处理 D. 在彩色图形显示器中,使用 RGB 颜色模型
解析:
光栅扫描显示器(raster scan)是按行、按像素点逐点刷新呈现图形,任何矢量图形都要先做“矢量—光栅”转换,再逐像素上色才显示,因此并非“按矢量直接描绘”也“不可能“不存在任何处理”。
其它选项均正确:图形文件系统用几何参数描述元素;图形处理精度与显示器分辨率无关;彩色显示器常用 RGB 模型。
以下关于图形变换的论述哪个是错误的?( B ) A. 平移变换不改变图形大小和形状,只改变图形位置 B. 错切变换虽然可引起图形角度改变,但不会发生图形畸变 C. 比例变换不改变图形的连接关系和平行关系 D. 旋转变换后各部分间的线性关系和角度关系不变,变换后直线的长度不变
解析:
错切(shearing)变换会保持平行关系,但会改变角度,且发生形状畸变(原角度≠90°,图形被“倾斜”)。
其它变换特性均正确:平移不改大小形状;比例保持连接、平行;旋转保持长度与角度。
透视投影中主灭点最多可以有几个?( D ) A. 0 B. 1 C. 2 D. 3
解析:
三维空间中,物体在三个主方向(对应 x、y、z 轴)的平行线各有一个灭点,故最多可有 3 个主灭点。
下列哪一个变换不是有关规范化投影变换?( C ) A. 错切变换 B. 旋转变换 C. 透视变换 D. 平移变换
解析:
规范化投影变换通常包括:错切、旋转、平移(用于将观察体变换到单位立方体视景体)。透视变换则是投影本身,不属于“规范化”步骤。
在三维空间中,绕任意轴进行旋转变换时,首先将该直线平移到使其经过原点,然后经过( D )变换,可以使得该直线与Y轴重合。 A. 绕 x 轴旋转 B. 绕 Y 轴旋转 C. 绕 Z 轴旋转 D. 先绕 x 轴旋转,再绕 Z 轴旋转
解析:
要将任意轴对齐 Y 轴,首先平移使该轴过原点,然后需先绕 x 轴旋转使该轴转到 x–z 平面内,接着再绕 z 轴旋转至与 Y 轴重合。
二、填空题
常用的直线生成算法是 DDA 算法 和 Bresenham 算法。
用于减少或克服在光栅图形显示器上绘制连续图形时,由离散量表示连续量引起的失真的技术叫 抗锯齿(Anti‑Aliasing)。
在平面几何投影可分为两大类:平行投影 和 透视投影。
分辨率是指屏幕在水平方向和垂直方向上能分辨的 最小可辨单元(像素)。
分辨率为 2048 × 1024,能显示 256 种颜色的显示器,至少需要选用帧缓存容量为
2048 × 1024 像素 × 8 位/像素 = 2 097 152 字节
彩色显示器使用 RGB 颜色模型,而彩色打印机使用 CMYK**== 颜色模型。
在图形文件中,常用 矢量方式 来描述图形元素(点、线、圆、弧等);而在光栅扫描图形显示器中,采用 光栅方式 显示所有图形。
当三维物体用透视变换方程投影到观察平面上,不与观察平面平行的任何一簇平行线投影成收敛线,其收敛点为 主灭点;物体中平行于某一坐标轴的平行线的灭点为 该坐标轴的灭点(如 X 轴灭点、Y 轴灭点或 Z 轴灭点)。
三、简答题
通过对比中点画线算法、DDA 算法以及 Bresenham 算法,分别论述这三个算法出现的背景,以及每个算法都做了哪些改进?举例说明各自都有哪些适用用场景。
解:
算法 背景 核心改进 适用场景 DDA 算法 数字微分分析(Digital Differential Analyzer)思想引入,将增量变化离散化 采用增量累加方式,使用浮点加法与取整 简单、易理解,适用于教学演示和精度要求低的软件绘制 中点画线算法 在 DDA 基础上,引入决策参数的概念 以中点位置决定下一个像素,减少一次取整运算 软件实现较多,可在 CPU 上高效运行 Bresenham 算法 为减少浮点运算与取整开销 彻底使用整数决策变量,增量更新更高效 硬件与嵌入式系统中最常用;实时性要求高时首选 改进脉络:
DDA 用浮点运算,计算量大;
中点算法引入决策参数,减少浮点→整数取整;
Bresenham 完全用整数,加速更明显。
举例:
在桌面 CAD 软件中,若对性能要求不高可用 DDA;
在游戏或嵌入式显示中,多用 Bresenham 以保证高帧率;
教学演示或算法分析常用中点算法,便于展示决策参数思想。
齐次坐标是什么?请举例说明如果在二维变换中不使用齐次坐标会产生什么问题。
定义:齐次坐标是在原来坐标基础上增加一个分量 w,将二维点 (x, y) 表示为三维向量 (x, y, w)。常用规范化形式为 (x,y,1)(x, y, 1)(x,y,1)。
如果不使用齐次坐标会产生的问题:
无法用矩阵统一表达平移——二维线性变换都可用 2×2 矩阵表示,但平移必须加法实现,无法与旋转、缩放等通过连乘合并;
复合变换麻烦——在无齐次坐标时,平移要单独处理,无法同线性变换一起做矩阵“连乘”优化;
透视变换也需除 w 操作,齐次坐标为透视投影提供了统一框架。
四、计算题
请使用 Cohen-Sutherland 算法裁剪直线段 p_1p_2
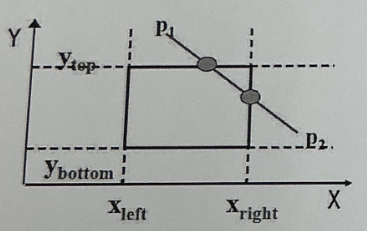
解:
一、设置区域码(Out‐code)
按位顺序 (Top, Bottom, Right, Left):
对 P_1(x_1,y_1):
若 y_1 > Y_{top} 则 Top 位=1,否则=0;
若 y_1 < Y_{bottom} 则 Bottom 位=1,否则=0;
若 x_1 > X_{right} 则 Right 位=1,否则=0;
若 x_1 < X_{left} 则 Left 位=1,否则=0。
题中 P_1 在上边外部 ⇒ 区域码 code(P_1)=1000_2。
对 P_2(x_2,y_2): 类似地,已知 P_2 在右边外部 ⇒ 区域码 code(P_2)=0010_2。
因为 code(P_1) & code(P_2)=0,且二者非零,进入裁剪循环。
二、第一次裁剪——处理 P_1(Top 位)
取出 P_1 的最高为 1 的那一位:Top ⇒ 与 y=Y_{top} 求交。
参数化直线:
x=x_1+t(x_2-x_1),y=y_1+t(y_2-y_1).
求 y=Y_{top} 时的参数
t_{top}=\frac{Y_{top}-y_1}{y_2-y_1}.
得到交点
P'_1=(x_1+t_{top}(x_2-x_1),Y_{top}).
更新:将 P_1 ← P'_1,重新计算其区域码(此时肯定落入矩形内部 ⇒ code=0000)。
三、第二次裁剪——处理 P_2(Right 位)
取出 P_2 的最高为 1 的那一位:Top ⇒ 与 x=X_{right} 求交。
用相同参数化,求
t_{right}=\frac{X_{right}-x_1}{x_2-x_1}.
得到交点
P'_2=(x_{right},y_1+t_{right}(y_2-y_1)).
更新:将 P_2 ← P'_2,重新计算其区域码(亦落入内部 ⇒ code=0000)。
四、裁剪结果
此时两端点区域码均为 0000,算法结束。 裁剪后线段在矩形内部的部分就是
P'_1=(x_1+\frac{Y_{top}-y_1}{y_2-y_1}(x_2-x_1),Y_{top}) --> P'_2=(x_{right},y_1+\frac{X_{right}-x_1}{x_2-x_1}(y_2-y_1))
请使用 Liang-Barsky 算法裁剪直线段 AB。
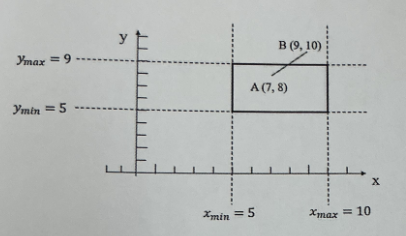
解:
我们以 A(7, 8) 为 P_0,B(9, 10) 为 P_1,窗口为 x∈[5, 10],y∈[5, 9],计算如下:
设 dx=x_1–x_0= 2 ,dy = y_1–y_0= 2。
定义四组 (p_i, q_i):
p_1= –dx = –2 , q_1=x_0-x_{min}=7-5=2
p_2= +dx = 2 , q_2=x_{max}-x_0=10-7=3
p_3= –dy = –2 , q_3=y_0-y_{min}=8-5=3
p_4= +dy = 2 , q_4=y_{max}-y_0=8-8=1
初始化 u₁ = 0,u₂ = 1。依次处理 i=1…4:
i=1:p_1<0 ⇒ u₁ = max(u_1,q_1/p_1)= max(0, 2/(–2)=–1) = 0
i=2:p_2>0 ⇒ u₂ = min(u_2,q_2/p_2)= min(1, 3/2=1.5) = 1
i=3:p_3<0 ⇒ u₁ = max(u_1,q_3/p_3)= max(0, 3/(–2)=–1.5) = 0
i=4:p_4>0⇒ u₂ = min(u_2,q_4/p_4)= min(1, 1/2=0.5) = 0.5
最终可视参数范围为 u∈[u_1=0,u_2=0.5 ]。
计算裁剪后端点:
当 u=u_1=0 时:P = (7 + 0·2, 8 + 0·2) = (7, 8)
当 u=u_2=0.5 时:P = (7 + 0.5·2, 8 + 0.5·2) = (8, 9)
结论:被裁剪后的线段在窗口内的部分是从 (7, 8) 到 (8, 9)
- 微信
- 赶快加我聊天吧

- 赶快加我聊天吧
