算法学习之前缀和与差分数组
这是一道,我再贴一下题目:
给你一个整数数组
nums,返回 数组answer,其中answer[i]等于nums中除nums[i]之外其余各元素的乘积 。题目数据 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。请 不要使用除法,且在
O(n)时间复杂度内完成此题。示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
一开始思路很简单,就是暴力的解法,使用两次循环,外层遍历每一个元素,内层分别对所有其他元素进行乘积。但是一看时间复杂度是 O(n^2),题目要求 O(n),便放弃该思路。题目里又说了不能使用除法,也断绝了直接求所有元素的乘积再除去各自元素的想法。
现在我想出了一个解法,思路是使用两个数组来记录前缀积和后缀积。假设我的输出结果叫做 res[],那么,这个 res 中的任意元素,比如,res[i] 的值 ,就是等于nums[0]到nums[i-1]的乘积,乘上,nums[i+1]到 nums[n-1]的乘积,只要定义两个数组就好了,分别是:
前缀积(曼巴?left):
left[i]存储数组nums中从 0 到i-1的所有元素的乘积。比如,left[0] = 1,而 i > 0 时,left[i]= left[i - 1] * nums[i - 1]
后缀积(right):
right[i]存储数组nums中从i+1到n-1的所有元素的乘积。比如,right[n-1] = 1,而 i < n-1 时,right[i]= right[i + 1] * nums[i + 1]
所以,任意一个我们要求的结果就是 res[i] = left[i] * right[i]
下面,给出我的代码,productExceptSelf 方法就是我的具体代码。
import java.util.Arrays;
/**
* @Author: sangui
* @CreateTime: 2025-11-14
* @Description:
* @Version: 1.0
*/
public class Q_238 {
public static void main(String[] args) {
// case1
int[] nums = {1, 2, 3, 4};
int[] res = productExceptSelf(nums);
// [24,12,8,6]
System.out.println(Arrays.toString(res));
// case2
// int[] nums = {-1, 1, 0, -3, 3};
// int[] res = productExceptSelf(nums);
// // [0,0,9,0,0]
// System.out.println(Arrays.toString(res));
}
public static int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] left = new int[n];
int[] right = new int[n];
int[] res = new int[n];
left[0] = 1;
for (int i = 1; i < n; i++) {
left[i] = left[i - 1] * nums[i - 1];
}
System.out.println("left:" + Arrays.toString(left));
right[n - 1] = 1;
for (int i = n - 2; i >= 0; i--) {
right[i] = right[i + 1] * nums[i + 1];
}
for (int i = 0; i < n; i++) {
res[i] = left[i] * right[i];
}
System.out.println("right:" + Arrays.toString(right));
return res;
}
}程序很清晰,我定义了三个数组,分别是 left 前缀积,right 后缀积,和 res 结果。时间复杂度是 3n,即 O(n),空间复杂度是也 3n,即 O(n)。符合题目预期。
2. 空间优化
还是基于上一题,提出一个空间优化,我们之前的程序中,存在定义三个数组,进一步优化空间,我们不创造新的数组,只定义 res 数组。虽然复杂度也还是 O(n),但这能很好得锻炼算法思维。
注意到:在之前,我们对 left 数组进行遍历求值的额时候,求哪个元素,只依赖 left 的上一个元素和 num 数组,而 left 数组一开始的值我们是 1;同样的,right 数组遍历求值得时候,也只是依赖 right 数组得上一个元素和 num 数组,而 right 数组的一开始的值我们是知道的,就是 1,所以完全不需要额外构建 left、right 数组,所以可以构建一个只有 res 的数组。但第一个程序也是很好的,它能帮我们提供一个很好的思路,就是前缀积和后缀积,这个思路也就是我们这个程序的思路。下面看我给出的空间优化后的程序,即 productExceptSelf2 方法。
public static int[] productExceptSelf2(int[] nums) {
int n = nums.length;
int[] res = new int[n];
res[0] = 1;
for (int i = 1; i < n; i++) {
res[i] = res[i - 1] * nums[i - 1];
}
System.out.println("res:" + Arrays.toString(res));
int rightValue = 1;
for (int i = n - 2; i >= 0; i--) {
rightValue *= nums[i + 1];
res[i] *= rightValue;
}
return res;
} 这个程序中只定义了一个额外的数组 res。但这不是 O(1) 的空间复杂度,如果我们能不额外构建数组,比如在原数组上修改就是 O(1) 了。在我的代码中,用到了 两个循环,可以看作是上一个程序中求 left 数组和 right 数组的两个循环的对应。看第一个循环,很好理解,做的事情和求 left 数组几乎一样,是前缀积。再看第二个循环,他是在算好前缀积的基础上进行修改的,从末尾开始,依次乘上 nums 的累乘。
3. 区域和检索-数组不可变
这同样是的一道题,看一下题目:
计算索引
left和right(包含left和right)之间的nums元素的 和 ,其中left <= right实现
NumArray类:
NumArray(int[] nums)使用数组nums初始化对象
int sumRange(int i, int j)返回数组nums中索引left和right之间的元素的 总和 ,包含left和right两点(也就是nums[left] + nums[left + 1] + ... + nums[right])示例 1:
输入:
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出:
[null, 1, -1, -3]
解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
乍看这题不明所以,格式有点复杂,其实很简单,这道题主类是 NumArray ,程序会自动创建它的一个实例,创建的时候会引入一个 nums 数组,然后系统会自动调用它的实例的 sumRange 方法,检索它的指定区间内的所有值的和。
这个题目用暴力也是最直接的方法,依次遍历求出每一个区间内的和就行,但明显不是题目要我们做的,复杂度过高。
我们还是额外创建一个数组,用于保存 nums 的前缀和,取名 prefix[]。这样到时候我们要求区间内的所有值的时候就可以:prefix[right]-prefix[left] ,这样就可以了。
import java.util.Arrays;
/**
* @Author: sangui
* @CreateTime: 2025-11-14
* @Description:
* @Version: 1.0
*/
public class Q_303 {
public static void main(String[] args) {
int[] nums = {-2, 0, 3, -5, 2, -1};
NumArray obj = new NumArray(nums);
// case1
// int left = 0;
// int right = 2;
// int res = obj.sumRange(left, right);
// // 1
// System.out.println(res);
// case2
// int left = 2;
// int right = 5;
// int res = obj.sumRange(left, right);
// // -1
// System.out.println(res);
// case3
int left = 0;
int right = 5;
int res = obj.sumRange(left, right);
// -3
System.out.println(res);
}
static class NumArray {
int[] prefix;
public NumArray(int[] nums) {
int n = nums.length;
this.prefix = new int[n + 1];
for (int i = 0; i < n; i++) {
prefix[i + 1] = prefix[i] + nums[i];
}
System.out.println(Arrays.toString(prefix));
}
public int sumRange(int left, int right) {
return prefix[right+1] - prefix[left];
}
}
}看我的程序,我定义了一个数组 prefix ,但我定义的长度不是 n ,而是 n + 1,这个点很关键,后面我也会提到,因为假如说按照我们的设想,我们定义 prefix[i] 为 num[0] 到 nums[i] 之间的和,那么返回结果为:prefix[right]-prefix[left] ,这个时候,返回结果里就会多减去一个 nums[left] 的值,这是,我们则需要在 sumRange 方法里额外获知 nums[left] 是多少,但此时我们不知道 nums[] 具体值,也不知道要获取 num[?],要知道必须引入额外的数组存储全部 nums[]。于是,我定义 prefix[i] 为 num[0] 到 nums[i-1] 之间的和,prefix[0] = 0,那么就得定义长度为 n + 1,而最终的结果也应该是:prefix[right + 1]-prefix[left] 。prefix[right + 1] 对应 num[0] 到 nums[right] 之间的和,prefix[left] 对应 num[0] 到 nums[left- 1] 之间的和。两者相减,就是 nums[left- 1] 到 nums[right] 之间的和。
4. 二维区域和检索-矩阵不可变
是上一题的而延伸,就是把检索的从一个一维区域,扩展到二维区域,大意还是没有变。我粘一下题目:
给定一个二维矩阵
matrix,以下类型的多个请求:
计算其子矩形范围内元素的总和,该子矩阵的 左上角 为
(row1, col1),右下角 为(row2, col2)。实现
NumMatrix类:
NumMatrix(int[][] matrix)给定整数矩阵matrix进行初始化
int sumRegion(int row1, int col1, int row2, int col2)返回 左上角(row1, col1)、右下角(row2, col2)所描述的子矩阵的元素 总和 。输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]
我的思路也还是没变,就是创建一个 prefix 的二维数组,这个数组的长度是 matrix 数组的长度 + 1,原因和上题一样,为了方便和省空间。这个 prefix 的定义是:prefix[i][j] = matrix[i-1][j-1] 到 matrix[0][0] 之间的数据和。
来看我的程序:
import java.util.Arrays;
/**
* @Author: sangui
* @CreateTime: 2025-11-14
* @Description:
* @Version: 1.0
*/
public class Q_304 {
public static void main(String[] args) {
int[][] matrix = {{3, 0, 1, 4, 2}, {5, 6, 3, 2, 1}, {1, 2, 0, 1, 5}, {4, 1, 0, 1, 7}, {1, 0, 3, 0, 5}};
NumMatrix obj = new NumMatrix(matrix);
// case1
int res = obj.sumRegion(2, 1, 4, 3);
// 8
System.out.println(res);
// case2
// int res = obj.sumRegion(2,1,4,3);
// // 8
// System.out.println(res);
// case3
// int res = obj.sumRegion(1,1,2,2);
// // 11
// System.out.println(res);
// case4
// int res = obj.sumRegion(1,2,2,4);
// // 12
// System.out.println(res);
}
static class NumMatrix {
int[][] prefix;
public NumMatrix(int[][] matrix) {
int m = matrix.length;
int n = matrix[0].length;
prefix = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
int lineCount = 0;
for (int j = 1; j <= n; j++) {
lineCount += matrix[i - 1][j - 1];
prefix[i][j] = prefix[i - 1][j] + lineCount;
}
}
System.out.println(Arrays.deepToString(prefix));
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return prefix[row2 + 1][col2 + 1] + prefix[row1][col1]-prefix[row1][col2+1]-prefix[row2+1][col1];
}
}
}主要就两点,就是:
我是如何计算 prefix 数组的
我是如何求区间的矩阵和值的
关于 prefix 数组,我的想法就是每一个元素的数据 = 上一行对应元素的数据 + 本行累计的数据和
关于求区间的矩阵和值,就是纯粹是数学上加减法(就是我的 sumRegion 方法),直接看我的表达式可能很复杂,但自己画个示意图就能很快明白,就是四个区域之间相加相减,得出中间的区域。
5. 子矩阵元素加 1
这个是今天(25-11-14)的,题目如下:
给你一个正整数
n,表示最初有一个n x n、下标从 0 开始的整数矩阵mat,矩阵中填满了 0 。另给你一个二维整数数组
query。针对每个查询query[i] = [row1i, col1i, row2i, col2i],请你执行下述操作:
找出 左上角 为
(row1i, col1i)且 右下角 为(row2i, col2i)的子矩阵,将子矩阵中的 每个元素 加1。也就是给所有满足row1i <= x <= row2i和col1i <= y <= col2i的mat[x][y]加1。返回执行完所有操作后得到的矩阵
mat。输入:n = 3, queries = [[1,1,2,2],[0,0,1,1]]
输出:[[1,1,0],[1,2,1],[0,1,1]]
解释:上图所展示的分别是:初始矩阵、执行完第一个操作后的矩阵、执行完第二个操作后的矩阵。
- 第一个操作:将左上角为 (1, 1) 且右下角为 (2, 2) 的子矩阵中的每个元素加 1 。
- 第二个操作:将左上角为 (0, 0) 且右下角为 (1, 1) 的子矩阵中的每个元素加 1 。
这个题看着像是第 4 题的相反,第四题是给你有值的二维数组,求某个区间的值得和。这一题是给你一些区间,求这个二维数组。在这一题中,要结合之前的几个程序,共同解决。
此题需用到 前缀和+ 二维差分,前缀和应该知道是什么,我第一题用的就是前缀,只不过是前缀积,第三、四题都用到了前缀和。而什么是二维差分?如果你按顺序看到这的话,实际上是接触过的,第三题就是一维差分,数组里的一维差分简单,只需要两个相减即可。而第四题用的就是二维差分,用在二维矩阵里。第四题中,我说的:
就是纯粹是数学上加减法(就是我的 sumRegion 方法),直接看我的表达式可能很复杂,但自己画个示意图就能很快明白,就是四个区域之间相加相减,得出中间的区域。
这个,其实就是二维差分。看我的示意图:
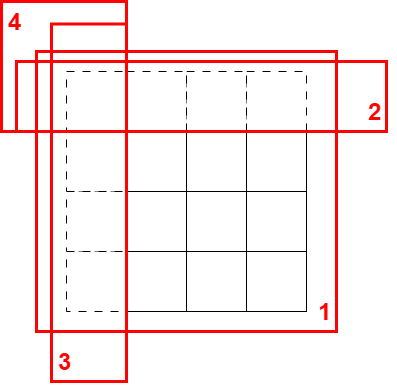
我们可以把二维差分比喻成一个计算面积的问题,比如说,我有个3 ×3 的正方形(如图的右下角的 3 × 3),该怎么计算面积呢,不要直接和我说得 9,我们可以通过增加 padding(在原 3 × 3 外围加一圈,使其变成 4 × 4)所以,原 3 ×3 的正方形的面积就等于:
1 的面积 - 2 的面积 - 3 的面积 + 4 的面积
当然了,正规的二维差分,它的 padding 一般是加在右下角的,我是打算强行和题解正规做法的区分开,毕竟原理是一样的。
那么问题来了,我们由求一个的面积转化为了四个的面积,这样会更好吗?
其实更快,我们通过之前学过的 前缀和 的方法,不需要真的求,通过前缀和来求这四个的面积,我们通过引入一个 diff 二维矩阵,来计算这四个的面积。
我们定义我们的矩阵为 diff[n+1][n+1](扩展成 n + 1 的原因这下就更清晰了),它的具体定义是:diff[i][j] 的值代表从 diff[0][0] 到 diff[i][j] 的区间里,所有的各自的值。最后,根据我的”求面积的公式“,得出我们 3 ×3 的正方形的面积。我的程序如下:
import java.util.Arrays;
/**
* @Author: sangui
* @CreateTime: 2025-11-14
* @Description:
* @Version: 1.0
*/
public class Q_2536 {
public static void main(String[] args) {
// case1
// int n = 3;
// int[][] queries = {{1, 1, 2, 2}, {0, 0, 1, 1}};
// int[][] res = rangeAddQueries(n, queries);
// // 预计输出:[[1,1,0],[1,2,1],[0,1,1]]
// System.out.println(Arrays.deepToString(res));
// case2
int n = 2;
int[][] queries = {{0, 0, 1, 1}};
int[][] res = rangeAddQueries(n, queries);
// 预计输出:[[1,1],[1,1]]
System.out.println(Arrays.deepToString(res));
}
public static int[][] rangeAddQueries(int n, int[][] queries) {
int[][] res = new int[n][n];
int[][] diff = new int[n + 1][n + 1];
for (int[] singleQuery : queries) {
int x1 = singleQuery[0] + 1;
int y1 = singleQuery[1] + 1;
int x2 = singleQuery[2] + 1;
int y2 = singleQuery[3] + 1;
// 大矩形
diff[x2][y2]++;
// 左边的一个小矩形
diff[x2][y1 - 1]--;
// 上边的另一个小矩形
diff[x1 - 1][y2]--;
// 多减去的左上角矩形,要恢复,即++
diff[x1 - 1][y1 - 1]++;
}
for (int i = n; i >= 1; i--) {
for (int j = n; j >= 1; j--) {
if (i != n) {
diff[i][j] += diff[i + 1][j];
}
if (j != n) {
diff[i][j] += diff[i][j + 1];
}
if (j != n && i != n) {
diff[i][j] -= diff[i + 1][j + 1];
}
res[i - 1][j - 1] = diff[i][j];
}
}
return res;
}
}程序的 rangeAddQueries 中大致可分为两部分,分别是两个循环:
第一个循环是为了给 diff 赋值。
第二个循环是为了给结果 res 赋值。
第一部分,根据我的面积法的二维差分的定义,来加减我的 diff 差分数组。
第二部分,这一部分是前缀和的应用,此时我们已经划分好了 diff 差分数组,我们从 右下角 到 左上角 的遍历方式。我的遍历规则如下:
若此时遍历的不是最底下的那一行,则累加此 diff 值为此行下一行对应位置的 diff 值;
若此时遍历的不是最右边的那一列,则累加此 diff 值为此列右边一列对应位置的 diff 值;
若此时遍历的既不是最底下的那一行,也不是最右边的那一列,则累减此 diff 值为右下角一格位置的 diff 值(因为该点被加了两次,我们只需要累加一次就够);
最后,我再把对应的 res 值赋上,注意坐标偏移。
好,我今天就先讲到这里,谢谢大家!
- 微信
- 赶快加我聊天吧

- 赶快加我聊天吧

2025年11月15日 16:16:33 1楼
三桂来点打家劫舍系列
2025年11月15日 18:37:04 1层
@ 格式 可以,我看看